7-1 最大子列和问题

给定K个整数组成的序列 $\lbrace N_1,N_2,\cdots,N_k \rbrace$，“连续子列”被定义为$\lbrace N_i,N_{i+1},\cdots,N_j \rbrace$，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

  • 数据1：与样例等价，测试基本正确性；
  • 数据2：102个随机整数；
  • 数据3：103个随机整数；
  • 数据4：104个随机整数；
  • 数据5：105个随机整数；

输入格式:
输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。

输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

1
2
6
-2 11 -4 13 -5 -2

解法一：存放在数组中，一个一个来比较

时间复杂度为：$T(n)=O(n^2)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<stdio.h>

int main(){
    int i,j,n,max=0,sum=0;
    scanf("%d",&n);
    int a[n];
    for(i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    for(i=0;i<n;i++){
        //每一趟
        for(j=i;j<n;j++){
            sum+=a[j];
            if(sum>max){
                max=sum;
            }
        }
        sum=0;
    }
    printf("%d",max);
    return 0;
}

解法二：联机实现

时间复杂度为：$T(n)=O(n)$

步骤：

  1. 先进行初始化，max赋0
  2. 再从头开始累加，加到大于最大子序列和的值，把这个值给MaxSum
  3. 如果累加为负数，这一小段的最大子序列就已经出来了，可以重新进行累加比较了
  4. 最后MaxSum一定为最大子序列的和

这题的关键：只要是首位元素为负数的肯定不是最大子列的组成部分，我们可以将其抛弃。即如果某个子列的首位为负数，那么它一定要借助后面的非负数。所以如果前面的n项是负数的话，后面的K-n项和一定会比K项和要大，所以在遇到前n项和是负数时，直接将和置0，从n+1项重新开始加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;
int a[100001];
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &a[i]);
    int sum = 0, maxsum = 0;
    for (int i = 0; i < n; i++)
    {
        sum += a[i]; //依次向右累加
        if (sum > maxsum)
            maxsum = sum; //更新最大值
        else if (sum < 0)
            sum = 0; //如果当前和为负数，那么后面的和会减小，所以需要新的起点。
    }
    printf("%d\n", maxsum);
    return 0;
}

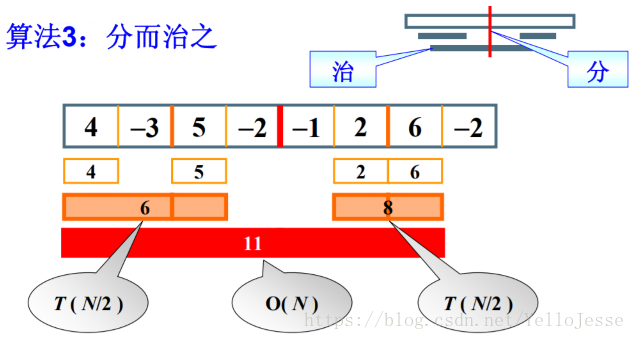
解法三：分治法

首先，我们可以把整个序列平均分成左右两部分，答案则会在以下三种情况中：

  1. 所求序列完全包含在左半部分的序列中。
  2. 所求序列完全包含在右半部分的序列中。
  3. 所求序列刚好横跨分割点，即左右序列各占一部分。

前两种情况和大问题一样，只是规模小了些，如果三个子问题都能解决，那么答案就是三个结果的最大值。

我们主要研究一下第三种情况如何解决：

我们只要计算出：以分割点为起点向左的最大连续序列和、以分割点为起点向右的最大连续序列和，这两个结果的和就是第三种情况的答案。因为已知起点，所以这两个结果都能在O(N)的时间复杂度能算出来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <stdio.h>

//N是数组长度，num是待计算的数组，放在全局区是因为可以开很大的数组
int N, num[16777216];

int solve(int left, int right)
{
    //序列长度为1时
    if(left == right)
        return num[left];
    
    //划分为两个规模更小的问题
    int mid = left + right >> 1;
    int lans = solve(left, mid);
    int rans = solve(mid + 1, right);
    
    //横跨分割点的情况
    int sum = 0, lmax = num[mid], rmax = num[mid + 1];
    for(int i = mid; i >= left; i--) {
        sum += num[i];
        if(sum > lmax) lmax = sum;
    }
    sum = 0;
    for(int i = mid + 1; i <= right; i++) {
        sum += num[i];
        if(sum > rmax) rmax = sum;
    }

    //答案是三种情况的最大值
    int ans = lmax + rmax;
    if(lans > ans) ans = lans;
    if(rans > ans) ans = rans;

    return ans;
}

int main()
{
    //输入数据
    scanf("%d", &N);
    for(int i = 1; i <= N; i++)
        scanf("%d", &num[i]);

    printf("%d\n", solve(1, N));

    return 0;
}