内容杂且多，老师讲的也一言难尽，用的吴恩达的PPT，也没有用全，跳着讲，公式也不解释清楚变量，推导也不推，照着ppt念，太难了QAQ
这里仅记录较为重要的部分

一些概念

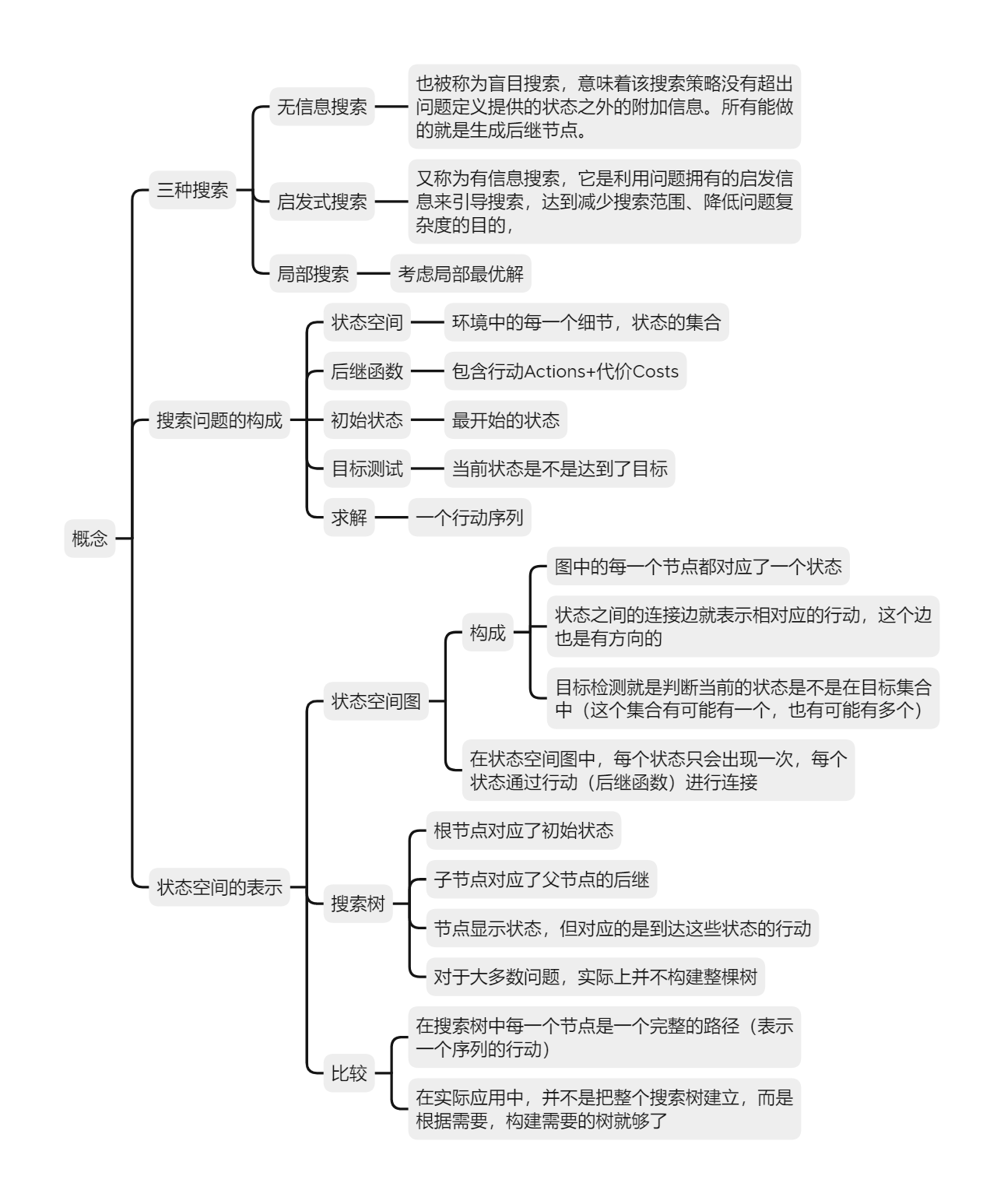
无信息搜索

无信息搜索也被称为盲目搜索，意味着该搜索策略没有超出问题定义提供的状态之外的附加信息。所有能做的就是生成后继节点。

深度优先搜索DFS

描述：每一次将深度最深的那个节点进行优先探索，若不是终点，则将其拓展并将它的子节点纳入边缘空间，若是边缘空间中所有的节点都是同一个深度，那么就探索最左边的那个节点
优点：机器每次只需要探索最深的那个点，而且边缘空间中的节点也不会太多，不会占用太多的内存
缺点：无法保证完备性和最优性，比较耗费时间

广度优先搜索BFS

描述：与深度搜索不同的是它每次拓展的是边缘空间节点中最浅的那个节点，都是同一个深度的话就拓展最左边的那个节点
优点：具备完备性
缺点：占用内存，而且也不具备最优性

DFS和BFS比较

迭代深入搜索

特点：同时结合深度优先于广度优先的优点
描述：预先设定一个探索的层数，然后在这个层数以内采用深度优先算法，当在这个层数里面都没有找到终点的话，然后就对这个层数进行拓展，允许进行更深一层的探索
优点：结合FDFS空间优势+BFS时间优势
缺点：可能会造成一定的浪费冗余

代价敏感搜索

特点：算法开始关注了路程中的代价问题，两个节点之间的代价不再等效处理

代价一致搜索

特点：代价敏感搜索的一种，一致代价搜索总是扩展路径消耗最小的节点N。N点的路径消耗等于前一节点N-1的路径消耗加上N-1到N节点的路径消耗

启发式搜索

启发式：对每个状态估计到最近目标的距离

贪婪搜索

策略：扩展你认为最接近目标状态的节点，只使用启发函数来评价节点
缺点：只考虑了后半段的距离而没有考虑前面的距离，不能满足最优性

A*算法（重要）

算法介绍

特点：结合贪婪搜索与代价一致搜索
策略：将代价函数g(n)与启发函数h(n)简单相加，得到一个新的函数f(n)，这个函数就是A*算法判断路径的标准
估价函数：f(n)=g(n)+h(n)，其中：g(n)是到达n节点已花费的代价；f(n)是当前节点到目标节点最小代价路径的估计值（greedy）
存在问题：当启发函数h大于实际耗散时，启发函数失效

可采纳性

1	0 ≤ h(n)≤ h*(n)

其中：h*(n) 是从 n 结点到目标结点的最优路径的真实代价，当启发式函数 h(n) 满足以上不等式的时候，我们称该 h(n) 是可采纳的 (admissible) ，即：没有过高估计某点到目标点的花费。

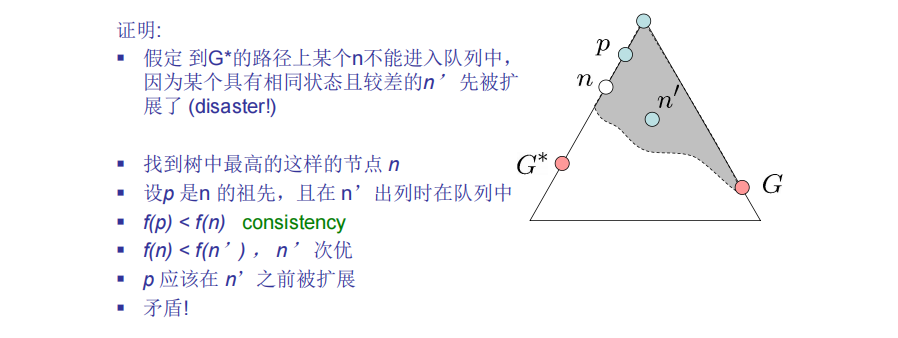
证明A* 树搜索的最优性（重要）

A*算法其他性质

Open表中任一具有f(n)<=f*(S0)的节点n，都被A*算法作为扩展节点

最优条件

树A*算法最优条件：可采纳性（h(n)<=h*(n)）
图A*算法最优条件：一致性（f(n)沿着路径非递减）

A*图搜索

主要思想

可采纳性：h(A)<=h*(A)真实
一致性：沿路径的节点f(n)值单调递增 h(A)<=cost(A to C)+h©

最优性

条件

一致性：

A*算法扩展节点，f值单调增
对于每个状态S，到达S最优的节点先于次优的节点扩展

证明

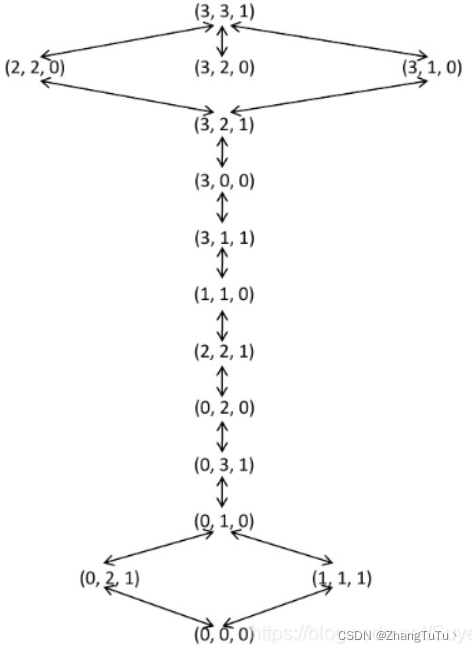
传教士和野人问题的A*搜索

变量解释：
M-左岸传教士数目
C-左岸野人数目
B-左岸是否有船
Pcm-有c个传教士，m个野人从左岸到右岸
Qcm-有c个传教士，m个野人从右岸到左岸

问题有解所必须的特性

M>=C且（3-M)>=(3-C)<==>M=C
或者M=0,M=3

安全状态(以左岸为例)：

传教士与野人的数目相等；
传教士都在左岸；
传教士都不在左岸。

完全状态图：
（不满足约束的不在图内）

参考: https://blog.csdn.net/qq_41296039/article/details/122442921?spm=1001.2014.3001.5501

局部搜索

爬山法：任意位置开始，可能是局部最优解；
模拟退火搜索：引入随机因素，避免局部极大；
遗传算法：适应度函数，每步保留N个最好状态。

其他

未知梯度时，用蚁群算法/粒子群算法；
贪婪最优搜索不是完备的。